Negative Decimal DWORD to Human Format

Introduction

This blog aims to ELI5, how negative numbers are stored in the Windows Registry, or any other DWORD for that matter. Why you may ask? Well, some keys like the SYSTEM\CurrentControlSet\Control\TimeZoneInformation\Bias, could well be a negative number. Which makes for some interesting CompSci Explanation.

NOTE: I love tables / Graphs / Visual aides, this will not be an in depth mathematical write-up, if you want the math, this isn’t the place

TLDR (Too Long Didn’t Read)

(If you want to read the full article, See Contents )

Reference

When checking a computer systems time drift, windows may keep a record of the computers drift from a server on the internet, as such its important to look at the following registry key in a DFIR Investigation for time correlation..

the HKLM\SYSTEM\CurrentControlSet\Control\TimeZoneInformation\ActiveTimeBias has a RegDWORD Value

This registry key is stored as a 32BIT, Unsigned, Little Endian, DWORD. For those not in the US (Anyone on a +x UTC Timezone) this key is stored as

UTC=Local Time + bias

Basically, windows knows how to interpret this key, but at first glance when you see 45781654 you might be thinking how, can that be actual minutes from UTC, are we on mars? No, we’re not on mars, we’re just dealing with how computers understand and store numbers, which like a martian is different to us.

But, its just a way to store data, a type of data, that windows understands, but a human doesnt quickly understand without conversion, to convert to a human readable format, you’ll need to do the below;

For those in a + timezone, we have a negative bias so need to calculate it, lets do it with the following key.

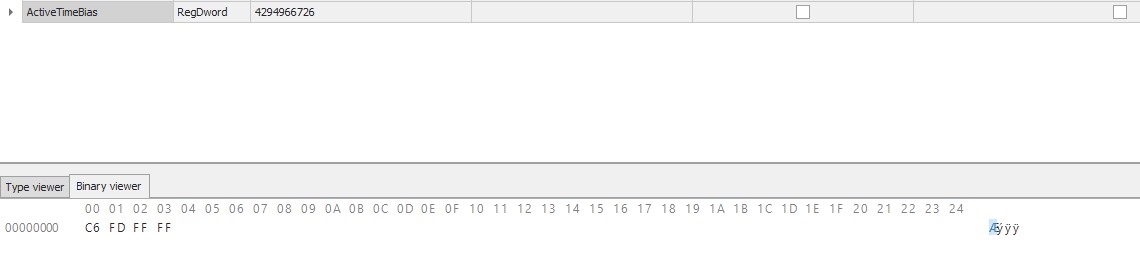
Little endian = C6 FD FF FF Big Endian = FF FF FD C6

Hexadecimal	Binary
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
A	1010
B	1011
C	1100
D	1101
E	1110
F	1111

Therefore FDC6 = x in binary

Hexadecimal	Binary
F	1111
D	1101
C	1100
6	0110

Therefore 1111 1101 1100 0110 in decimal

32768	16384	8192	4096	2048	1024	512	256	#	128	64	32	16	8	4	2	1
1	1	1	1	1	1	0	1	#	1	1	0	0	0	1	1	0

Drop the leading 0’s

1101 1100 0110

Remove the Leading 1’s notation (Flip the binary) + Convert to decimal

2048	1024	512	256	#	128	64	32	16	8	4	2	1
0	0	1	0	#	0	0	1	1	1	0	0	1
-	-	512	-	#	0	0	32	16	8	0	0	1

== 512 + 32 + 16 + 8 + 1 == -569

Add the Two’s compliment 1

== 512 + 32 + 16 + 8 + 1 == -570

Therefore

-570 / 60

= -9.5 HRS

Therefore (Flip for windows minus)

Timezone = +9.5 (OR (If time was 19:00 - 9.5HRS) == UTC)

Contents

• Introduction
• TLDR (Too Long Didn’t Read)
• Contents
• 1. What the hell is a DWORD anyway
• 0. What the hell is binary
• 1. So okay, what is this WORD thing all about then
• 2. Okay, so we have the puppies, now what? (Data in words)
• 3. Cool, numbers are stored by binary, what happens in a dword
• 4. Damn, thats a lot of numbers, or more emoji for my keyboard, so what about negative numbers
• 5. The magical 39 05 00 00 number, or, hexadecimal
• 6 The next gotcha Endian
• 6.1 The great binary to decimal conversion
• 7. Signed / Unsigned Numbers, the great negative number
  • 7.1 Unsigned Numbers (Windows DWORD’s)
• 8 Okay, all that effort, so what

1. What the hell is a DWORD anyway

Oh, well, I’m glad you asked. Unfortunately it is not a duck in the registry (D_Word… See what i did there), Nor is it actually a word. No, like many things in computing the name is not necessarily representative of the function… yay, but there is some background here. To do this were going to need to get a little nerdy with binary… ruh roh, i hear you say, its okay ELI5…

Wait, so perhaps we should start with

0. What the hell is binary

-Reference

Yeah, okay, this is a fair point what is binary. Well, see that computer, or for that matter anything with a switch like below?

Well, that I (or 1) is on and that O is off, notice the similarity, thanks to those electrical engineers, we kept some sense on this.

So, a computer, which essentially works by a lot of little switches (very simplistically) uses 1’s and 0’s to represent data, just as you and i speak english, and don’t understand martian language, any human language is about as foreign to a computer as an alien language if they invaded us tomorrow.

1. So okay, what is this WORD thing all about then

Yup, computers don’t understand english, yet were talking about binary words, oh dear, no wonder this gets confusing, hang in there. So a computer that just looks at a 1 or 0 (A Bit) wouldn’t be that interesting. So some engineers got together in the 70’s and wanted to encode some text into binary, they decided they needed 255 characters to store every character on a keyboard, this is something called ASCII, to do this with a computer, they needed a combination of 8 Bits, and now we have a byte.

As time went on, and we wanted more complex data in our computers, like emoji’s engineers decided to double this to two bytes, or a word. And so inventively, as more time went on, and we wanted more data, we finally decided not to reinvent the wheel, and just call a piece of data that was twice the size of a word a double word.

Okay, lets recap here with a nice table picture

2. Okay, so we have the puppies, now what? (Data in words)

Cool, so we know that binary stores 1’s and 0’s in a bit, so what is a byte firstly, everything stored on a computer, is a number, even you’re text that you’re reading on this screen is actually a number (Remember that ASCII thing from before?). For now we really want to keep it to numbers, so lets get back to the numbers

Binary stores stores numbers depending on the format you ask for, but in the most basic form, this is in a byte (remember puppo chewing on you’re laptop?)

To convert decimal to binary (no, im not appeasing you budding mathematicians… were keeping it simple, no powers here) we basically double each number. If you’ve ever bought computer hardware, or seen anything with a computer, you’ve likely seen these numbers. Lets for now keep it small at the number 9 to decimal

128	64	32	16	8	4	2	1
0	0	0	0	1	0	0	1

This actually equals nine, lets explain why

When working with binary, we work from the left, and keep taking the remainder off, well, at least i do, but perhaps im weird as im a visual learner.

This means, that we start from the left until we can sub tract something

1. 9 - 128 = 0 (0 means i cant)
2. 9 - 64 = 0
3. 9 - 32 = 0
4. 9 - 16 = 0
5. 9 - 8 = 1 (1 Means i can, Subtract 8, 1 left)
6. 1 - 4 = 0
7. 1 - 2 = 0
8. 1 - 1 = 1 (1 Means i can, now i have 0 left)

Lets do this one more time, so it makes more sense, with a number like 12

128	64	32	16	8	4	2	1
0	0	0	0	1	1	0	0

1. 12 - 128 = 0 (0 means i cant)
2. 12 - 64 = 0
3. 12 - 32 = 0
4. 12 - 16 = 0
5. 12 - 8 = 1 (1 Means i can, subtract 8, 4 left)
6. 12 - 4 = 1 (1 Means i can, subtract 4, 0 stop)
7. 12 - 2 = 0 (no more numbers left)
8. 12 - 1 = 0 (no more numbers left)

3. Cool, numbers are stored by binary, what happens in a dword

So, for a dword we essentially have the same thing, but a lot longer, remember how we wanted to store those emoji before?

Word, really dont want to see how big a dword is, for now, lets keep it at the word level, but if you want to, keep getting your last result * 2

32768	16384	8192	4096	2048	1024	512	256	#	128	64	32	16	8	4	2	1
0	0	0	0	0	0	0	0	#	0	0	0	0	0	0	0	0

4. Damn, thats a lot of numbers, or more emoji for my keyboard, so what about negative numbers

Okay, so now again we get more complicated, as we need to discuss a couple more concepts…. yay

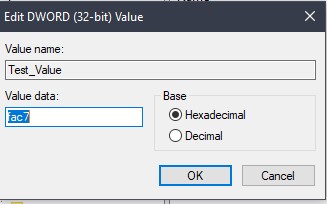
So, in a DWORD, a positive number is simple, it works the same way as we’ve seen above. To demonstrate i’ll show a windows registry value below with the number 1337

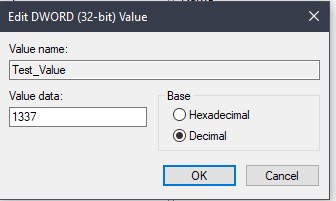
Now, lets see this data stored with a forensics tool to see the raw data.

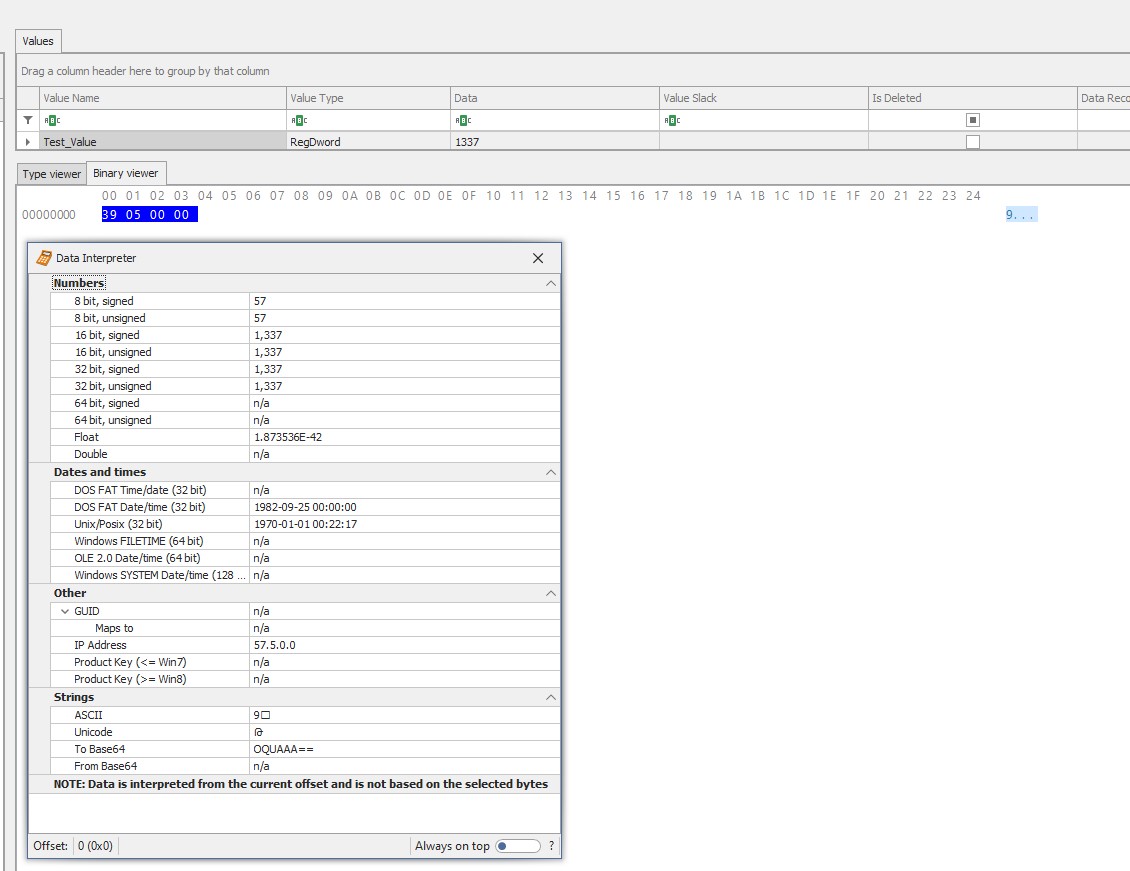
Whoah, what, i swear we skipped a few steps there, i hear you say, what are we looking at i hear you say… you explination su….. shh… patience its coming ;-)

So, we can see our ever important 1337 number but what the hell is that 39 05 00 00 number and this stuff about signed, unsigned etc, do i have to print the registry and sign it. Please, dont print you’re registry, you’re going to have a bad time

Let’s explain

5. The magical 39 05 00 00 number, or, hexadecimal

Im no math person, infact i hate math, i think way too visually to enjoy math. So, am i going to teach you hexadecimal, another counting system. No…..

What i will give though, is a basic conversion table, as i loooove tables, or calculators. From here you will see though that hexadecimal is another weird way of counting.

But, the table shall come soon, lets talk WHY there is hexadecimal represented here.

Remember this?

Well turns out we have a handy dandy way of representing data to a human, who really wants to read lots of binary, unless you’re a robot

So, lets jump back to our word example from before

Hexadecimal counts to 16, notice thats half a byte?

128	64	32	16	#	8	4	2	1
0	0	0	0	#	1	1	0	0

This data can actually be represented in hex, to make it easier for a human ro read. (Finally that afformentioned table)

Hexadecimal	Decimal	Binary
0	0	0000 0000
1	1	0000 0001
2	2	0000 0010
3	3	0000 0011
4	4	0000 0100
5	5	0000 0101
6	6	0000 0110
7	7	0000 0111
8	8	0000 1000
9	9	0000 1001
A	10	0000 1010
B	11	0000 1011
C	12	0000 1100
D	13	0000 1101
E	14	0000 1110
F	15	0000 1111

Whoa, new counting system eh, now thats a mind blow moment, notice though, how that makes a very nice representation of the second half of they byte, how much easier is it to read that than 1101?

Now, to bring this back, when using this method in binary, we can see that a hexadecimal value, can only represent half a byte, so, you need two hexadecimal values together to show all the bytes.

Dont worry about making a table bigger than this, we WONT need it, unless you’re a math person, in which case im sure you’ve already cringed at my explanation and left. Okay so lets work with this….

6 The next gotcha Endian

As if this wernt enough windows likes to store its data in little endian

Okay, as an english speaker, you read right to left yes? well russians read left to right. This goes the same for how windows stores a DWORD. (Before you hate, simple peeps, simple, i dont want to scare people off with Significant bits OKAY!!)

Don’t fret though for our explication (Missing a whole lot of stuff, This disclaimer has been placed so some compsci professor doesn’t backhand me), even though memory reads left to right, its only a little harder than russian. Basically, notice how for such a small number we have heaps of 0’s?

with 39 05 00 00, that itself would mean a huge number when looking at our aforementioned table

32768	16384	8192	4096	2048	1024	512	256	#	128	64	32	16	8	4	2	1
0	0	0	0	0	0	0	0	#	0	0	0	0	0	0	0	0

Lets make this the right way round, its easy

Little endian = 39 05 00 00 Big Endian = 00 00 05 39

Notice how now, we seem to have a nice small number? being 0539? lets do something with this

Hexadecimal	Binary
0	0000
5	0101
3	0011
9	1001

= 0000 0101 0011 1001

Wait, you say, thats a word!! and in this case you’d be correct, if this was a DWORD, you’d want a calculator, but this is easy to work with. (You’ll notice i’ve dropped the decimal…. its coming, mathematicians may hate me, but visual guy here keeps it simple)

6.1 The great binary to decimal conversion

Okay, so we got rid of the endianness (The way computers read data vs a human (Comp Sci prof screeching in corner)) Now, lets convert that binary to decimal, using the handy dandy table for words

32768	16384	8192	4096	2048	1024	512	256	#	128	64	32	16	8	4	2	1
0	0	0	0	0	1	0	1	#	0	0	1	1	1	0	0	1
-	-	-	-	-	1024	-	256	#	-	-	32	16	8	-	-	1

= 1024 + 256 + 32 + 16 + 8 + 1 = 1337

Wow, we have our value back, after all that russian (endian) and weird counting system (hex), so whats this signed/unsigned thing?

7. Signed / Unsigned Numbers, the great negative number

• Reference

A computer, with a DWORD can read between 0 - 4294967295. Notice this number has no room for negative numbers. This is where signed and unsigned numbers come in.

A signed integer is a little more fancy, it can actually store a negative number, a 0 and positive numbers (–2147483648 to +2147483647), within a DWORD this isn’t used a lot in windows from references I can find.

7.1 Unsigned Numbers (Windows DWORD’s)

• References

• 

A DWORD is unsigned, which means to represent negative numbers, it has a series of 1’s in front of it.

Using our example from before, did you notice how the following occured?

Little endian = 39 05 00 00

Big Endian = 00 00 05 39

Thats a lot of wasted zero’s right, what if i told you they had another purpose? We’ll, there is, unfortunately someone had to invite the mathematician to the table, and give it a name called Two’s Compliment. You could read wikipedia, and get confused with

if the binary number 0102 encodes the signed integer 210, then its two's complement, 1102, encodes the inverse: −210. In other words, to reverse the sign of most integers (all but one of them) in this scheme, you can take the two's complement of its binary representation.[2] The tables at right illustrate this property. 

Okay, Human time

Firsly to convert binary to a 1’s compliment, we flip the 1’s into zeros (Dont worry, 2 is coming)

Lets keep it simple first, and represent 9

128	64	32	16	8	4	2	1
0	0	0	0	1	0	0	1

So Negative lets firstly flip to 1’s compliment

128	64	32	16	8	4	2	1
1	1	1	1	0	1	1	0

To make this number into a 2’s compliment add one

So Negative lets firstly flip to 1’s compliment

128	64	32	16	8	4	2	1
1	1	1	1	0	1	1	1

There you go, you now have a negative number represented in binary with the 2’s compliment, wasn’t that hard right? But why?

Well I’m glad you asked…

128	64	32	16	8	4	2	1
1	1	1	1	0	1	1	0

Take the FIRST 1, before a zero, and use that as the negative number. Keep the rest as positive numbers, and, you’ll verify you’re original number

= (-16) 0 + 4 + 2 + 1 = -9

Remember, this is just a way for a computer to understand its a one, there are other contexts around this beyond this tutorial.

Okay, lets now try with our 1337….

= 1024 + 256 + 32 + 16 + 8 + 1 = 1337

32768	16384	8192	4096	2048	1024	512	256	#	128	64	32	16	8	4	2	1
0	0	0	0	0	1	0	1	#	0	0	1	1	1	0	0	1

Now, lets go to a one compliment (Flip those bits)

32768	16384	8192	4096	2048	1024	512	256	#	128	64	32	16	8	4	2	1
1	1	1	1	1	0	1	0	#	1	1	0	0	0	1	1	0

Now, to a two’s compliment (add one)

32768	16384	8192	4096	2048	1024	512	256	#	128	64	32	16	8	4	2	1
1	1	1	1	1	0	1	0	#	1	1	0	0	0	1	1	1

Verify you’re input….

32768	16384	8192	4096	2048	1024	512	256	#	128	64	32	16	8	4	2	1
-	-	-	-	-2048	-	512	-	#	128	64	-	-	-	4	2	1

=(-2048) + 512 + 128 + 64 + 4 + 2 + 1 = 1337

Now, to convert to the Hex

Hexadecimal	Binary
F	1111
A	1010
C	1100
7	0111

1111	1010	1100	0111
F	A	C	7

Big Endian = 00 00 FA C7 Little endian = C7 FA 00 00

Lets see if the conversions are right in the registry key (Note, registry keys are stored in Human (Big endian, When entering a value)

8 Okay, all that effort, so what

See TLDR (Too Long Didn’t Read)